A Biologically Modeled Computational Paradigm
Nature tends to find the most efficient path forward. The thoughtful may observe and learn from nature’s ingenuity and employ these methods in the development of technology whenever possible.
The system that nature has devised for encoding and transmitting complex information is known as genetics where information is encoded through the use of RNA and DNA. Has the time come to employ nature’s own information management system in the field of modern computer science? Could doing so bring about a useful transformation in the state of art for computing machines?
Brief Summary of DNA Structure
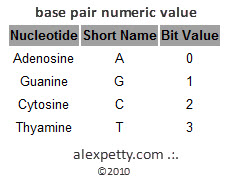
DNA is a four bit system using the following nucleic acids as units for storing and conveying data.
These are:
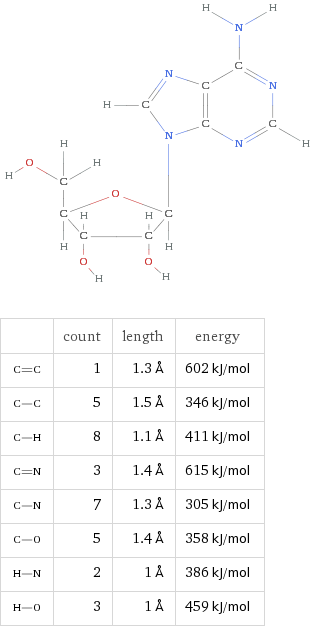
Adenosine (A)
Formula C10H13N5O4
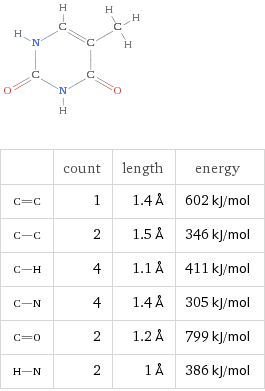
Thyamine (T)
Formula C5H6N2O2
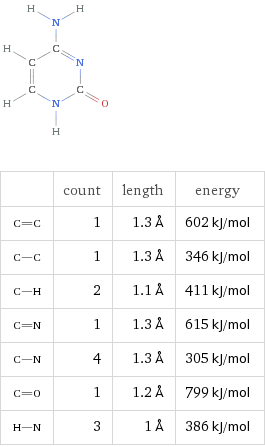
Cytosine (C)
Formula C4H5N3O
Guanine (G)
Formula C5H5N5O
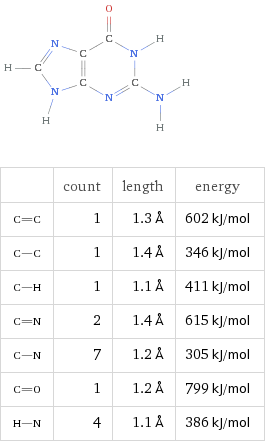
By virtue of their geometry, which is governed by opposing polar forces, these nucleic acids will always pair such that Adenosine binds with Thyamine and Cytosine with Guanine. These units are referred to as base pairs.
Possibility of a DNA-Modeled Computing Paradigm
The basis of modern computer science is binary in nature, which is to say that it is based upon whether the voltage in a given transistor is off (zero) or on (one). These zeros and ones are rolled up into a base 2 number system which is operated to encode information “digitally”. By convention (e.g. standards like ASCII or UTF8), the letters of the English alphabet, for example, are digitally encoded by 8-bit phrases of zeros and ones called bytes.
DNA is also digital, but it is not limited to positions 0 and 1. DNA uses 4 possible bit positions and is, therefore, a quaternary digital system:
By convention, a binary digital byte is 8 bits in length, providing 256 possible different values per byte.
A “byte” of DNA is called a codon. A codon is 3 bits long (e.g., AAA or GCT). Each bit can be one of 4 possible values (0, 1, 2 or 3) and so the DNA quaternary encoding system provides 64 possible values per codon.
Binary 8 Bit Byte
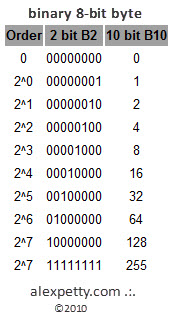
Any value between 0 and 255 can be expressed within this binary system. For example, the number 73 would include 1 bit from 2^6, 1 bit from 2^3 and 1 bit from 2^0.
This binary value looks like:
01001001
and can be expressed in base 10 as:
64 + 8 + 1 = 73
Quaternary 3 Bit Byte (aka. Codon)
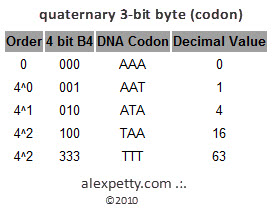
Any value between 0 and 63 can be expressed within this quaternary system.
For example, the number 53 is represented by a 3 bit in the 4^2 ordinal, a 1 bit in the 4^1 ordinal and a 0 bit in the 4^0 ordinal. This is represented as 310 in base 4. Chemically, DNA would express this with the use of the following nucleic acids:
TGA which would pair with ACT.
Complete listing of codon bit pairs (All sum to 9)
The positive side (left) and the negative side (right) sum to 9, which represents a stable neutrality. This polar balance provides the underlying framework dictating DNA’s physical form. It is the magnetic relationship between the base pairs that enables the compression of DNA in biological systems. The very same principles, when encoded numerically, provide an underpinning for a DNA-modeled compression algorithm.
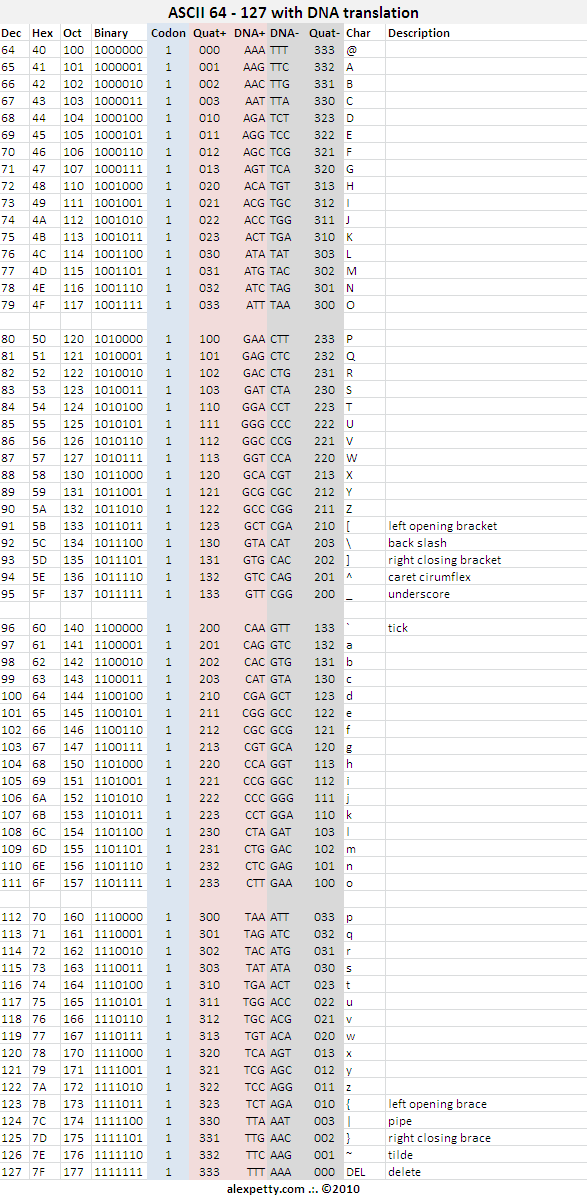
Keyboard Encoding Standard
ASCII standard encoding with DNA translation
The longtime standard for keyboard encoding is known as ASCII. Since ASCII is a base-2 8-bit standard, it supports 256 unique values. Just as a 16-bit binary standard requires 2 bytes to cover a range of 512 characters, a DNA-based keyboard encoding standard, with its limit of 64 values per codon, requires multiple codons to support the ASCII standard. This can be implemented as follows:
Codon 0
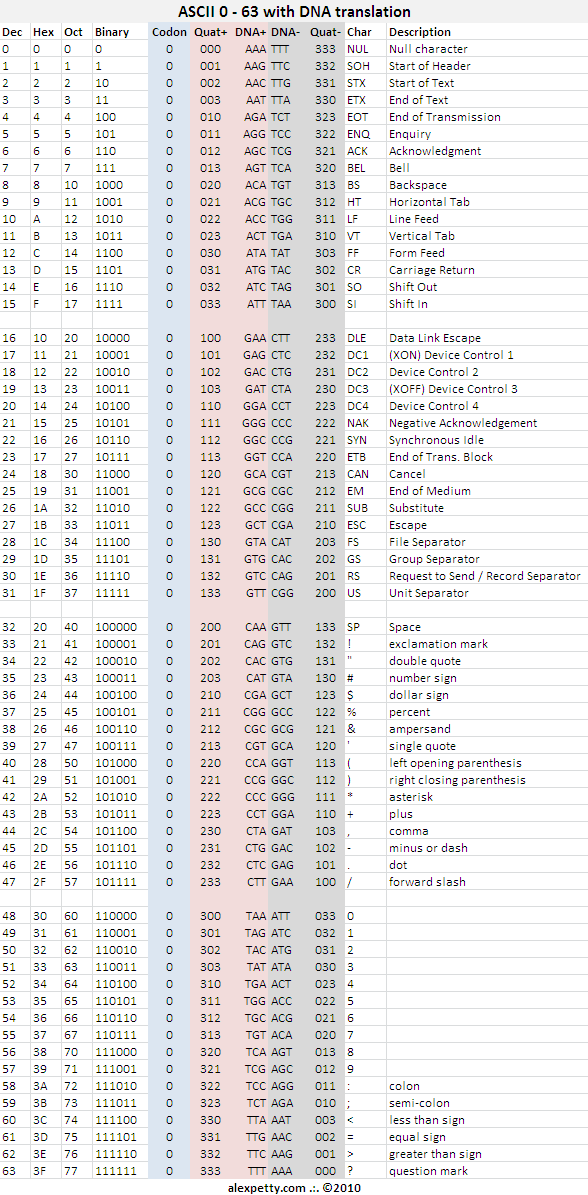
Codon 1
New Foundational Standards
It would be ideal to deprecate many of the legacy ASCII character codes such as ENQ, RS, EM, etc in a new DNA based standard.
In developing a new Foundational Encoding Standard, UTF8, UTF16, etc. should be considered. It may take as many as 8 codons to capture all of the needed keyboard codes for worldwide requirements.
Simple Encoding Example
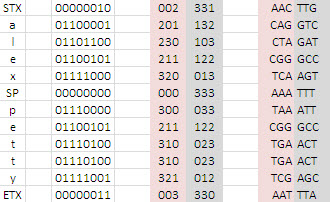
Only one half of the codon pair needs to be stored since the other half can be inferred and applied by an algorithm at compression runtime.
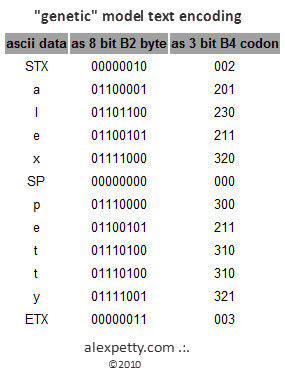
The ability to persist only half the bit pair provides a fundamental efficiency quotient of 3 to 8 (62.5%) over the current binary paradigm before compression is even considered.
Numeric Polarity based Helical Compression Algorithm
Using these methods, data can be compressed in a manner identical to that of DNA. It is possible to utilize the idea of “numeric polarity” to compress information into a kind of “chromosomal superstructure” just as with physical DNA.
Furthermore, it appears that DNA modeled compression offers performance curves allowing large amounts of information to be more tightly packed then smaller amounts of information. This agrees with the observation that fruit fly DNA is physically much larger than human DNA and yet it contains many orders of magnitude less data.
DNA Runtime Environment
32 bit PC architecture allows the CPU to address four 8-bit bytes of data per clock cycle. Since a quaternary system is not compatible with today’s hardware, a translation layer is required which may be implemented as a runtime environment.
Bit position 9 is reserved for technical overhead to support the virtual run-time environment. The 9th bit can be reclaimed when implemented on quaternary based hardware.
I should also note that, while I am proposing a system of bits based on 0, 1, 2, 3 for the sake of feasibility of implementation. The system nature itself uses appears to rely on the following pairing system :
1 pairs with 8
2 pairs with 7
and 4 pairs with 5
9 is apparently an expression of polar neutrality.
3 and 6 may be connected to negative and positive poles.
CMYK Data Transmission
The subtractive CMYK four-state color description system appears to operate in a manner similar to that of how nature uses light within physical RNA/DNA. A kind of “technical access” to the use of 1-8, 2-7 and 4-5 pairs may be achievable using a light-based system. It could be possible to input and output quaternary digital information to DNA-modeled machines using light harmonics in the form of a subtractive 4 color standard.
C = Cyan
M = Magenta
Y = Yellow
K = key (Black)
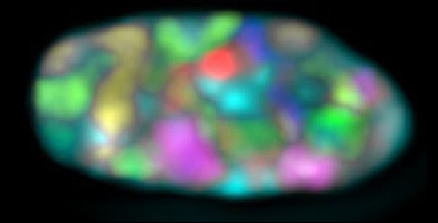
It is interesting to note that chromosomes (tightly packed DNA superstructures) naturally reflect these same colors, thus their name. Below is an image of the colors reflected by a chromosome in the presence of white light.
.:.
